学籍番号　　　　　　　　　　　　　　学科　　　　　　　　講座　氏名　　　　　　　　　　　

１．

1.1　20mはかったつもりが実は19.99mであったというメジャーなので，一辺計測する毎に19.99/20.00の補正が必要である．土地の面積がa x b (m²)で計測されたとすると，真の面積はab (19.99/20.00)²となる．a x bが200m²なので，求める面積は199.8 m²

1.2　三平方の定理から，　すなわち，

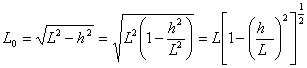
となる．ここで展開を行い，第三項以降が極めて微少なので第二項までとれば，

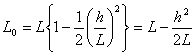
２．

2.1 「視準軸誤差」，「水平軸誤差」，「鉛直軸誤差」．前者二つは正反の読みで相殺できるが，鉛直軸誤差は消去することが出来ない．

2.2

測線	方位	距離 [m]	緯距　[m]		経距 [m]
			＋	―	＋	―
AB	N54゜45’ E	65.0	37.5		53.1
BC	S70゜15’ E	87.4		-29.5	82.3
CD	S15゜30’ W	80.7		-77.8		-21.6
DA	N58゜15’ W	133.5	70.2			-113.5

0.4 0.3

閉合差：　SQRT(0.3^2+0.4^2)=0.5　　　閉合比：733分の1 0.00136

3．

3.1　例えばある場所の位置と形を決めることが必要であったとして，距離測量と角測量そして多角測量の計算を使って物の形を厳密に求める．これらの測量は目的とする場所の形や位置を決める物なので高い精度が要求される．ついで平板測量を使って細部の測量を行う．平板測量は，現実の世界を相似な図形によって縮小して描くもので，測量の結果を図上に直に表していくことになる．測量としては簡易で，図の縮尺の関係から多少精度が粗くなる．

3.2　縮尺が1/1000なので平板測量で許される図上の誤差を0.2mmとすると0.2mm x 1000=200mmつまり20cmまでは誤差として図上には現れない．従ってA君の行っている平板測量で現実には問題は起こらない．

3.3　「示誤三角形」

４.

4.1　πラジアンが180°であるから，1rad=180x60x60/3.14…..= 206369　（3.14を使った場合） or 206265（関数πなどを使った場合） second.

4.2 正弦定理より，三角形ABPにおいて，

三角形ACPにおいて，. これよりsinB=B=0.0001rad sinC=C=0.000025rad となる（B,C共に微小角なので）．ここで三角形の内角の和は180度どうし，また対頂角は等しいから，辺ABPCで形作られる二つの三角形について，

角C＋角BAC=角B＋角BPC．先に求めた角BCがrad表示であることに注意して．

つまり角BAC=角B-角C+角BPC=200000”*(0.0001-0.000025)rad+60^o=60^o00’15”

５．

5.1　標尺1,2が持つ誤差をe₁,e₂とすると標尺は前視・後視で使われるため，高低差を求める作業では常に誤差が相殺される形（＋，−）で出現する。これを偶数回使えば誤差が残らないため，水準測量ではレベルを偶数回据え付け，最初に使ったスタッフを最後に使って終わるようにする。

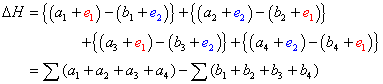
5.2 各水準環の閉合差δと観測の制限値Eを計算すれば次の通りである．

水準環�T δ1=(1)+(2)=-1.260+1.195=-6.5cm E1=1.0√(3+2.2)=2.3cm

水準環�U δ2=-(2)-(3)-(4)=-1.195-1.095-(-2.372)=+8.2cm E2=1.0√(2.2+1.9+2.2)=2.5cm

水準環�V δ3=(4)+(5)=-2.372+2.363=-0.9cm E3=1.0√(2.2+2)=2.0cm

水準環�T，�Uが制限を越えており，ここで共通の(2)が観測不良と推測される．

さらに

水準環�W δ4=(1)-(3)-(4)=-1.260-1.095-(-2.372)=+1.7cm E4=1.0√(3+1.9+2.2)=2.7cm

水準環�X δ5=(1)-(3)-(5)=-1.260-1.095+2.363=+0.8cm E5=1.0√(3+1.9+2)=2.6cm

水準環�Y δ6=-(2)-(3)+(5)=-1.195-1.095+2.363=+7.3cm E6=1.0√(2.2+1.9+2)=2.5cm

すなわち路線2を含まなければ観測制限値を越えない．

従って再測の必要があるのは(2)